Musik yang kita dengar setiap hari tidak lepas dari peran penting resonansi. Salah satu contoh resonansi yang paling memikat adalah pipa organa. Rumus pipa organa terbuka menjadi kunci dalam memahami rahasia di balik suara merdu instrumen ini.
Pipa organa terbuka memiliki panjang tertentu yang menentukan frekuensi resonansi yang dihasilkan. Dengan mengaplikasikan rumus matematika, kita dapat menghitung frekuensi tersebut dan mengeksplorasi prinsip akustik yang mendasarinya.
Pengertian Rumus Pipa Organa Terbuka

Rumus pipa organa terbuka adalah persamaan yang digunakan untuk menghitung frekuensi bunyi yang dihasilkan oleh pipa organa terbuka. Pipa organa terbuka adalah pipa dengan salah satu ujungnya terbuka ke udara luar, sementara ujung lainnya tertutup.
Ketika udara ditiupkan ke dalam pipa, udara akan bergetar dan menghasilkan bunyi. Frekuensi bunyi yang dihasilkan tergantung pada panjang pipa dan kecepatan suara di udara.
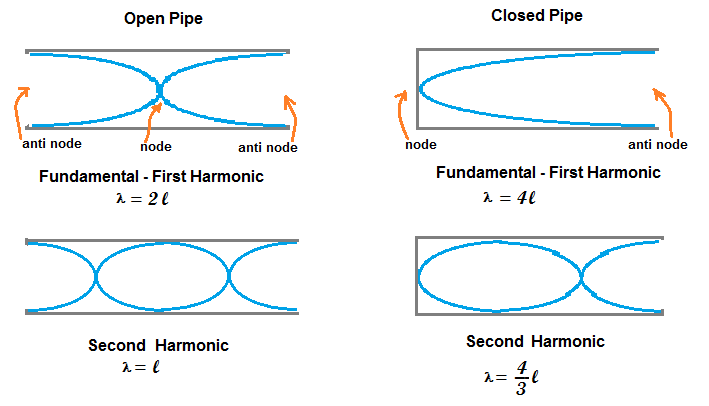
Perbedaan Pipa Organa Terbuka dan Tertutup
Pipa organa terbuka berbeda dengan pipa organa tertutup, yang memiliki kedua ujungnya tertutup. Pipa organa tertutup menghasilkan bunyi dengan frekuensi yang lebih rendah dibandingkan pipa organa terbuka dengan panjang yang sama.
Hal ini disebabkan karena udara di dalam pipa organa tertutup tidak dapat bergerak bebas seperti pada pipa organa terbuka. Akibatnya, udara di dalam pipa organa tertutup bergetar lebih lambat, menghasilkan frekuensi bunyi yang lebih rendah.
Turunan Rumus Pipa Organa Terbuka
Rumus pipa organa terbuka adalah:
$$f = \fracv4L$$
di mana:
* f adalah frekuensi nada (Hz)
- v adalah kecepatan suara (m/s)
- L adalah panjang pipa (m)
Turunan Rumus
- Mulai dengan persamaan gelombang berdiri pada pipa organa terbuka:$$f = \fracnv4L$$di mana n adalah jumlah simpul pada pipa (n = 1 untuk nada dasar).
- Untuk pipa organa terbuka, simpul terjadi pada ujung terbuka pipa. Jadi, n = 1.
- Substitusikan n = 1 ke dalam persamaan:$$f = \fracv4L$$
Keterbatasan dan Asumsi
- Turunan ini mengasumsikan bahwa pipa organa berbentuk silinder yang sempurna dan memiliki ujung yang tajam.
- Rumus ini tidak memperhitungkan efek gesekan atau viskositas pada udara di dalam pipa.
- Turunan ini juga mengasumsikan bahwa kecepatan suara konstan sepanjang pipa.
Penerapan Rumus Pipa Organa Terbuka
Rumus pipa organa terbuka banyak digunakan dalam berbagai bidang, mulai dari akustik hingga musik. Berikut adalah beberapa penerapannya:
Dalam Akustik
- Memprediksi frekuensi nada dasar pipa organa terbuka, yang penting dalam desain instrumen musik.
- Mendesain ruang konser dan auditorium untuk memaksimalkan kualitas suara.
- Menentukan panjang pipa yang diperlukan untuk menghasilkan nada tertentu dalam aplikasi industri, seperti sonar dan pengukur aliran.
Dalam Musik
- Menghitung panjang pipa organ untuk menghasilkan nada tertentu.
- Membuat dan menyetel alat musik tiup, seperti seruling, klarinet, dan saksofon.
- Menentukan frekuensi nada yang akan dihasilkan oleh pipa organa terbuka dengan panjang tertentu.
Keterbatasan dan Tantangan
Meskipun rumus pipa organa terbuka sangat berguna, ada beberapa keterbatasan dan tantangan dalam penerapannya:
- Rumus hanya berlaku untuk pipa organa terbuka, tidak untuk pipa tertutup atau sebagian tertutup.
- Rumus tidak memperhitungkan efek ujung, yang dapat mempengaruhi frekuensi nada dasar.
- Rumus tidak memperhitungkan suhu dan kelembaban, yang dapat mempengaruhi kecepatan suara dan panjang gelombang.
- Dalam situasi praktis, mungkin sulit untuk mengukur panjang pipa secara akurat, yang dapat menyebabkan kesalahan dalam perhitungan.
Variasi dan Modifikasi Rumus Pipa Organa Terbuka
Rumus pipa organa terbuka dapat dimodifikasi untuk mengakomodasi variasi bentuk dan kondisi pipa. Modifikasi ini memengaruhi frekuensi resonansi pipa, menghasilkan nada yang berbeda.
Pipa Organa Berujung Kerucut
Untuk pipa organa berujung kerucut, diameter pipa mengecil secara bertahap dari dasar ke atas. Modifikasi rumus adalah sebagai berikut:
f = (0,6 × v) / (4L + 2r)
di mana:
- fadalah frekuensi resonansi
- vadalah kecepatan suara
- Ladalah panjang pipa
- radalah radius dasar pipa
Pipa Organa Berujung Silinder
Untuk pipa organa berujung silinder, diameter pipa sama di sepanjang panjangnya. Modifikasi rumus adalah sebagai berikut:
f = (0,5 × v) / L
di mana:
- fadalah frekuensi resonansi
- vadalah kecepatan suara
- Ladalah panjang pipa
Implikasi Modifikasi
Modifikasi rumus pipa organa terbuka berdampak pada frekuensi resonansi pipa. Pipa dengan ujung kerucut memiliki frekuensi resonansi yang lebih tinggi daripada pipa dengan ujung terbuka yang sama panjangnya. Sebaliknya, pipa dengan ujung silinder memiliki frekuensi resonansi yang lebih rendah daripada pipa dengan ujung terbuka yang sama panjangnya.
Aplikasi Lanjutan Rumus Pipa Organa Terbuka
Rumus pipa organa terbuka tidak hanya terbatas pada menghitung frekuensi dasar, tetapi juga memiliki aplikasi yang lebih luas dalam desain instrumen musik.
Merancang Organ Pipa
Dalam merancang organ pipa, rumus ini digunakan untuk menentukan panjang pipa yang diperlukan untuk menghasilkan nada tertentu. Dengan mengontrol panjang pipa, pembuat organ dapat mengatur nada yang dihasilkannya, sehingga menciptakan beragam suara.
Merancang Klarinet
Rumus pipa organa terbuka juga diterapkan dalam desain klarinet. Klarinet adalah instrumen tiup kayu yang menggunakan reed untuk menghasilkan suara. Panjang pipa klarinet, yang disebut “barel”, mempengaruhi frekuensi nada yang dihasilkan. Dengan menyesuaikan panjang barel, pembuat klarinet dapat mengoptimalkan nada dan timbre instrumen.
Mengoptimalkan Frekuensi dan Timbre, Rumus pipa organa terbuka
Rumus pipa organa terbuka membantu desainer instrumen mengoptimalkan frekuensi dan timbre instrumen mereka. Dengan mengetahui hubungan antara panjang pipa dan frekuensi dasar, mereka dapat membuat instrumen yang menghasilkan nada tertentu dengan presisi tinggi.
Selain itu, rumus ini juga digunakan untuk menyesuaikan timbre instrumen. Dengan mengubah bentuk atau bahan pipa, desainer instrumen dapat memengaruhi harmonik yang dihasilkan, sehingga menciptakan suara yang khas dan unik.
Pemungkas

Rumus pipa organa terbuka tidak hanya menjadi alat yang ampuh dalam memahami resonansi, tetapi juga membuka jalan bagi inovasi dalam desain instrumen musik. Dengan mengoptimalkan panjang dan bentuk pipa, kita dapat menciptakan instrumen yang menghasilkan suara yang lebih kaya dan harmonis.
Sudut Pertanyaan Umum (FAQ)
Apa perbedaan antara pipa organa terbuka dan tertutup?
Pipa organa terbuka memiliki kedua ujung terbuka, sedangkan pipa organa tertutup hanya memiliki satu ujung terbuka.
Bagaimana cara menghitung frekuensi resonansi pipa organa terbuka?
Frekuensi resonansi dapat dihitung menggunakan rumus: f = v / 4L, di mana v adalah kecepatan suara dan L adalah panjang pipa.
