Contoh Jarak Titik ke Garis: Pengertian, Langkah, dan Aplikasinya

Contoh jarak titik ke garis – Dalam geometri, jarak titik ke garis merupakan konsep penting yang banyak digunakan dalam berbagai bidang. Apakah Anda ingin mengukur jarak rumah Anda ke jalan raya atau menghitung kemiringan atap, memahami jarak titik ke garis sangatlah krusial. Yuk, kita pelajari lebih dalam tentang konsep ini!

Jarak titik ke garis adalah jarak tegak lurus dari sebuah titik ke garis lurus. Ini mengukur seberapa jauh titik tersebut berada dari garis. Konsep ini dapat diaplikasikan dalam berbagai bidang, seperti arsitektur, teknik, dan matematika.

Pengertian Jarak Titik ke Garis

Dalam geometri, jarak titik ke garis adalah jarak terpendek antara suatu titik dan garis lurus. Jarak ini penting untuk menentukan posisi relatif titik dan garis, serta untuk memecahkan berbagai masalah geometri.

Rumus untuk menghitung jarak titik ke garis adalah:

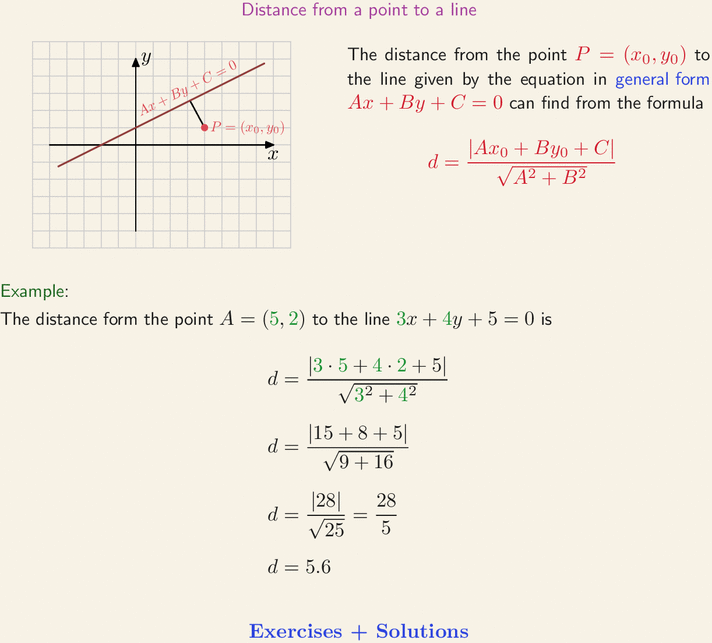
d = |Ax + By + C| / √(A² + B²)

di mana:

• d adalah jarak titik ke garis
• A, B, dan C adalah koefisien persamaan garis (Ax + By + C = 0)
• x dan y adalah koordinat titik

Langkah-Langkah Menentukan Jarak Titik ke Garis

Menentukan jarak titik ke garis merupakan langkah penting dalam geometri. Berikut langkah-langkah sistematis untuk menentukan jarak tersebut:

Menggambar Garis Tegak Lurus

• Gambarkan garis yang melalui titik dan tegak lurus terhadap garis yang diberikan. Garis ini disebut garis tegak lurus.
• Titik potong antara garis tegak lurus dan garis yang diberikan disebut titik kaki.

Menghitung Jarak Titik ke Garis Tegak Lurus

• Hitung panjang garis tegak lurus dari titik ke titik kaki. Ini adalah jarak antara titik dan garis tegak lurus.
• Jarak dari titik ke garis yang diberikan sama dengan jarak dari titik ke garis tegak lurus.

Ilustrasi

[Gambar garis, titik, garis tegak lurus, dan titik kaki. Jarak titik ke garis tegak lurus diberi label sebagai ‘d’.]

3. Contoh Soal dan Pembahasan

Untuk memperdalam pemahaman, berikut beberapa contoh soal jarak titik ke garis beserta pembahasannya:

Soal 1: Jarak Titik ke Garis Sederhana

Tentukan jarak titik P(2, 3) ke garis 2x + y – 5 = 0.

Pembahasan:

1. Tuliskan persamaan garis dalam bentuk y = mx + c:
• 2x + y- 5 = 0
• y = -2x + 5
2. Gunakan rumus jarak titik ke garis:
• d = |ax + by + c| / √(a² + b²)
• d = |2(2) + 3 – 5| / √(2² + 1²)
• d = 2 / √5

Soal 2: Jarak Titik ke Garis dengan Titik dan Vektor, Contoh jarak titik ke garis

Tentukan jarak titik Q(-1, 4) ke garis yang melalui titik A(1, 2) dan memiliki vektor arah .

Pembahasan:

1. Tentukan persamaan garis dalam bentuk vektor:
• r = A + tv
• r = (1, 2) + t(1, 1)
2. Gunakan rumus jarak titik ke garis dalam bentuk vektor:
• d = |(r- Q) · v| / |v|
• d = |((-1, 4) – (1, 2)) · (1, 1)| / √(1² + 1²)
• d = 3 / √2

Soal 3: Jarak Titik ke Garis Paralel

Tentukan jarak titik R(3, 1) ke garis yang sejajar dengan garis 3x – y + 2 = 0 dan berjarak 2 satuan.

Pembahasan:

1. Tentukan persamaan garis paralel:
• 3x- y + d = 0, di mana d adalah jarak ke garis
• 3x – y + 2 + d = 0, karena jaraknya 2 satuan
2. Gunakan rumus jarak titik ke garis:
• d = |ax + by + c| / √(a² + b²)
• d = |3(3) – 1 + 2 + d| / √(3² + 1²)
• d = 8 + d / √10
3. Karena jarak ke garis adalah 2, maka:
• 8 + d = 2√10
• d = 2√10 – 8

Aplikasi Jarak Titik ke Garis: Contoh Jarak Titik Ke Garis

Jarak titik ke garis memiliki aplikasi yang luas dalam berbagai bidang, termasuk arsitektur, teknik, dan matematika. Memahami cara menghitung jarak ini sangat penting untuk menyelesaikan berbagai masalah praktis dan teoritis.

Aplikasi dalam Arsitektur

Dalam arsitektur, jarak titik ke garis digunakan untuk:

• Menentukan jarak antara dinding dan perabotan untuk memastikan ruang yang optimal.
• Menghitung jarak aman antara bangunan dan jalan untuk meminimalkan risiko tabrakan.
• Memastikan jarak yang memadai antara jendela dan pintu untuk ventilasi dan pencahayaan yang tepat.

Aplikasi dalam Teknik

Dalam teknik, jarak titik ke garis digunakan untuk:

• Menghitung jarak antara titik pemasangan dan garis beban untuk menentukan tekanan dan tegangan pada struktur.
• Menentukan jarak aman antara kabel dan permukaan untuk mencegah korsleting.
• Menghitung jarak antara sensor dan objek untuk mengoptimalkan kinerja sistem.

Aplikasi dalam Matematika

Dalam matematika, jarak titik ke garis digunakan untuk:

• Menentukan persamaan garis yang melalui dua titik yang diberikan.
• Menemukan titik pada garis yang paling dekat dengan titik tertentu.
• Memecahkan sistem persamaan linier dan non-linier.

Memahami cara menghitung jarak titik ke garis sangat penting dalam berbagai bidang. Ini memungkinkan kita untuk menyelesaikan masalah praktis dan teoritis dengan akurat dan efisien.

Tabel Rumus Jarak Titik ke Garis

Untuk memudahkan perhitungan jarak titik ke garis, berikut tabel yang merangkum rumus-rumus yang dapat digunakan dalam berbagai kasus:

Garis Horizontal

• Rumus: d = |y – y ₁|
• Keterangan:
• d: jarak titik ke garis
• y: koordinat y titik
• y ₁: koordinat y garis

Garis Vertikal

• Rumus: d = |x – x ₁|
• Keterangan:
• d: jarak titik ke garis
• x: koordinat x titik
• x ₁: koordinat x garis

Garis Miring

• Rumus: d = |(Ax + By + C) / √(A ²+ B ²)|
• Keterangan:
• d: jarak titik ke garis
• A, B, C: koefisien persamaan garis (Ax + By + C = 0)
• x, y: koordinat titik

Ilustrasi Geometris

Ilustrasi geometris memberikan gambaran visual yang jelas tentang jarak titik ke garis. Dengan menggunakan titik, garis, dan segitiga siku-siku, kita dapat menunjukkan konsep ini dalam berbagai posisi dan orientasi.

Ilustrasi ini membantu kita memahami bahwa jarak titik ke garis adalah panjang segmen garis terpendek yang menghubungkan titik tersebut ke garis.

Contoh Ilustrasi

• Titik di atas garis:Segmen garis tegak lurus dari titik ke garis mewakili jarak.
• Titik di bawah garis:Sama seperti di atas, tetapi segmen garisnya tegak lurus ke bawah.
• Titik pada garis:Jarak titik ke garis adalah nol karena titik tersebut terletak tepat pada garis.
• Titik sejajar dengan garis:Jarak titik ke garis adalah panjang proyeksi titik ke garis.

Batasan dan Pengecualian

Rumus standar untuk menghitung jarak titik ke garis mungkin tidak berlaku dalam kasus-kasus tertentu. Berikut adalah beberapa batasan dan pengecualian:

Kasus Titik Berada pada Garis

Jika titik yang diberikan berada pada garis, maka jaraknya ke garis adalah 0.

Kasus Garis Paralel

Jika titik dan garis paralel, maka jaraknya adalah jarak tegak lurus antara titik dan salah satu titik pada garis.

Kasus Garis Berhimpitan

Jika titik dan garis berhimpitan, maka jaraknya adalah 0.

Kasus Titik Berada di Luar Bidang Garis

Jika titik berada di luar bidang yang ditentukan oleh garis, maka rumus standar tidak dapat digunakan untuk menghitung jaraknya. Dalam kasus ini, diperlukan metode alternatif seperti menggunakan vektor normal pada bidang garis.

Kasus Titik Berada pada Titik Singgung Garis

Jika titik berada pada titik singgung garis dan kurva lainnya, maka jaraknya ke garis adalah jarak tegak lurus antara titik dan kurva.

Simpulan Akhir

Memahami jarak titik ke garis tidak hanya bermanfaat dalam memecahkan soal geometri, tetapi juga memiliki aplikasi praktis di dunia nyata. Dengan memahami konsep ini, kita dapat merancang bangunan yang lebih efisien, mengoptimalkan proses produksi, dan bahkan memprediksi lintasan objek dalam fisika.

Jadi, jangan ragu untuk menguasai konsep jarak titik ke garis, karena pengetahuan ini akan membuka banyak pintu peluang bagi Anda!

Pertanyaan yang Sering Diajukan

Apa rumus jarak titik ke garis?

Rumus jarak titik ke garis adalah |Ax + By + C| / √(A² + B²), di mana (A, B) adalah vektor arah garis dan (x, y) adalah koordinat titik.

Bagaimana cara menentukan jarak titik ke garis yang sejajar sumbu x atau y?

Jika garis sejajar sumbu x, rumusnya menjadi |y – y1|, dan jika garis sejajar sumbu y, rumusnya menjadi |x – x1|, di mana (x1, y1) adalah koordinat titik pada garis.